ΤΥΠΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ ΠΙΝΑΚΩΝ
Υπολογισμός αθροισμάτων στοιχείων του πίνακα.
Παράδειγμα 1 (Μονοδιάστατο πίνακα)
Έστω πίνακας Π με τις μηνιαίες εισπράξεις (σε χιλιάδες ευρώ) για ένα έτος, ενός εστιατορίου.
Να υπολογίσετε το μέσο όρο των εισπράξεων των «κακών» μηνών (δηλαδή εκείνων των μηνών που οι εισπράξεις ήταν κάτω από 20000 ευρώ):
Λύση
ΣΥΝ ← 0 ΠΛ ← 0 ΓΙΑ i ΑΠΟ 1 ΜΕΧΡΙ 12 ΑΝ Π[Ι]<20 ΤΟΤΕ
ΣΥΝ ← ΣΥΝ + Π[i]
ΤΕΛΟΣ_ΑΝ
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΑΝ ΠΛ>0 ΤΟΤΕ ΜΟ ← ΣΥΝ/ΠΛ ΑΛΛΙΩΣ ΓΡΑΨΕ ”Κάθε μήνα οι εισπράξεις ήταν πάνω από 20000” ΤΕΛΟΣ_ΑΝ
Η τελευταία ΑΝ μπήκε για την περίπτωση που η μεταβλητή ΠΛ παραμείνει 0. Σε αυτή την περίπτωση η εκτέλεση της εντολής ΜΟ ← ΣΥΝ/ΠΛ θα οδηγούσε σε σφάλμα ( παραβίαση του κριτηρίου καθοριστικότητας).
Παράδειγμα 2 (Δισδιάστατο πίνακα)
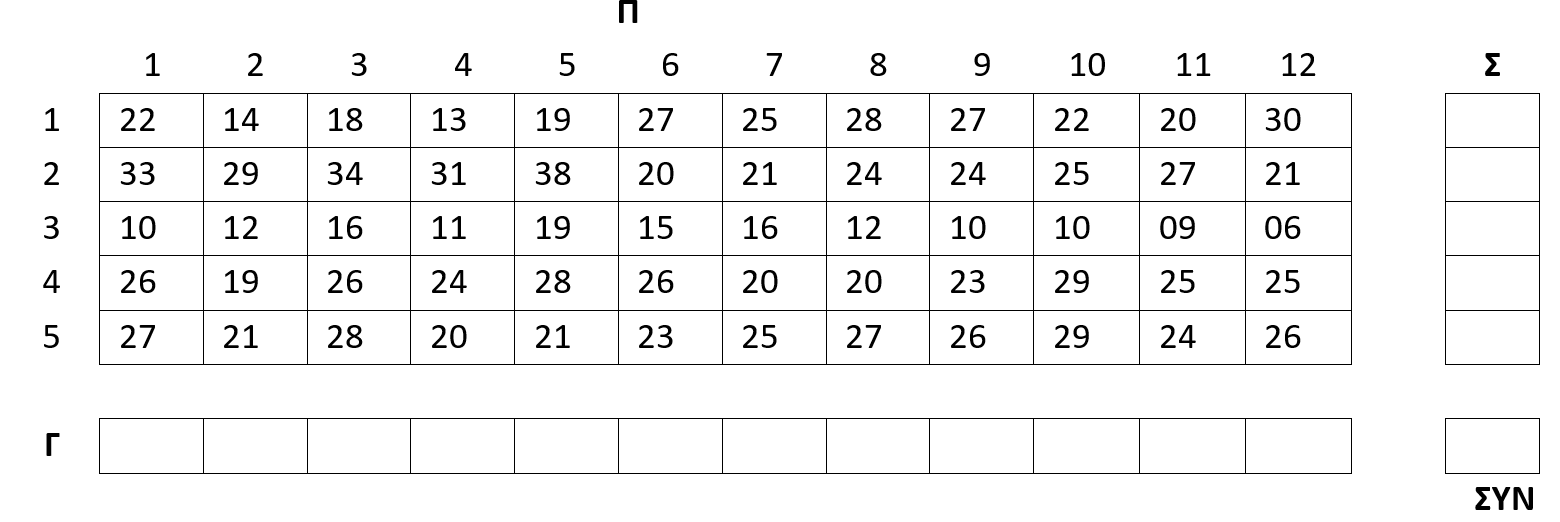
Έστω πίνακας Π με τις μηνιαίες εισπράξεις (σε χιλιάδες ευρώ) για ένα έτος, κάθε ενός από τα 5 καταστήματα μιας αλυσίδας εστιατορίων. Να υπολογίσετε:
- τις ετήσιες εισπράξεις κάθε εστιατορίου
- τις μηνιαίες εισπράξεις όλων των εστιατορίων μαζί
- τις συνολικές εισπράξεις όλων των εστιατορίων μαζί για ένα χρόνο.
Λύση
Για το πρώτο ερώτημα πρέπει να χρησιμοποιήσουμε ένα νέο μονοδιάστατο πίνακα Σ με 5 κελιά όπου κάθε κελί του θα περιέχει το άθροισμα των κελιών της αντίστοιχης γραμμής του πίνακα Π.
Για το δεύτερο ερώτημα απαιτείται πάλι μονοδιάστατος πίνακας Γ με 12 κελιά όπου κάθε κελί του θα περιέχει το άθροισμα των κελιών της αντίστοιχης στήλης του πίνακα Π.
Για το τρίτο ερώτημα απαιτείται μία μόνο μεταβλητή ΣΥΝ στην οποία θα εκχωρήσουμε το άθροισμα όλων των κελιών του πίνακα Π.
Ακολουθεί τμήμα προγράμματος που υλοποιεί τα παραπάνω για πίνακα Π με m γραμμές και n στήλες. Τα κελιά των πινάκων Σ και Γ πρέπει αρχικά να πάρουν την τιμή 0. Το ίδιο και η μεταβλητή ΣΥΝ.
ΣΥΝ ← 0
ΓΙΑ i ΑΠΟ 1 ΜΕΧΡΙ 5
Σ[i] ← 0
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΓΙΑ j ΑΠΟ 1 ΜΕΧΡΙ 12
Γ[j] ← 0
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΓΙΑ I ΑΠΟ 1 ΜΕΧΡΙ 5
ΓΙΑ J ΑΠΟ 1 ΜΕΧΡΙ 12
ΣΥΝ ← ΣΥΝ + Π[i,j]
Σ[i] ← Σ[i] + Π[i,j]
Γ[j] ← Γ[j] + Π[i,j]
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
Εύρεση του μέγιστου ή του ελάχιστου στοιχείου.
Παράδειγμα 3 (Μονοδιάστατο πίνακα)
Έστω ο πίνακας του παραδείγματος 1. Να βρείτε την μέγιστη μηνιαία είσπραξη του εστιατορίου.
Λύση
ΜΑΧ ← Π[1]
ΓΙΑ I ΑΠΟ 2 ΜΕΧΡΙ 12
ΑΝ ΜΑΧ <Π[Ι] ΤΟΤΕ
ΜΑΧ ← Π[Ι]
ΤΕΛΟΣ_ΑΝ
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
Ή εναλλακτικά
ΜΑΧ ← 0
ΓΙΑ I ΑΠΟ 1 ΜΕΧΡΙ 12
ΑΝ ΜΑΧ <Π[Ι] ΤΟΤΕ
ΜΑΧ ← Π[Ι]
ΤΕΛΟΣ_ΑΝ
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
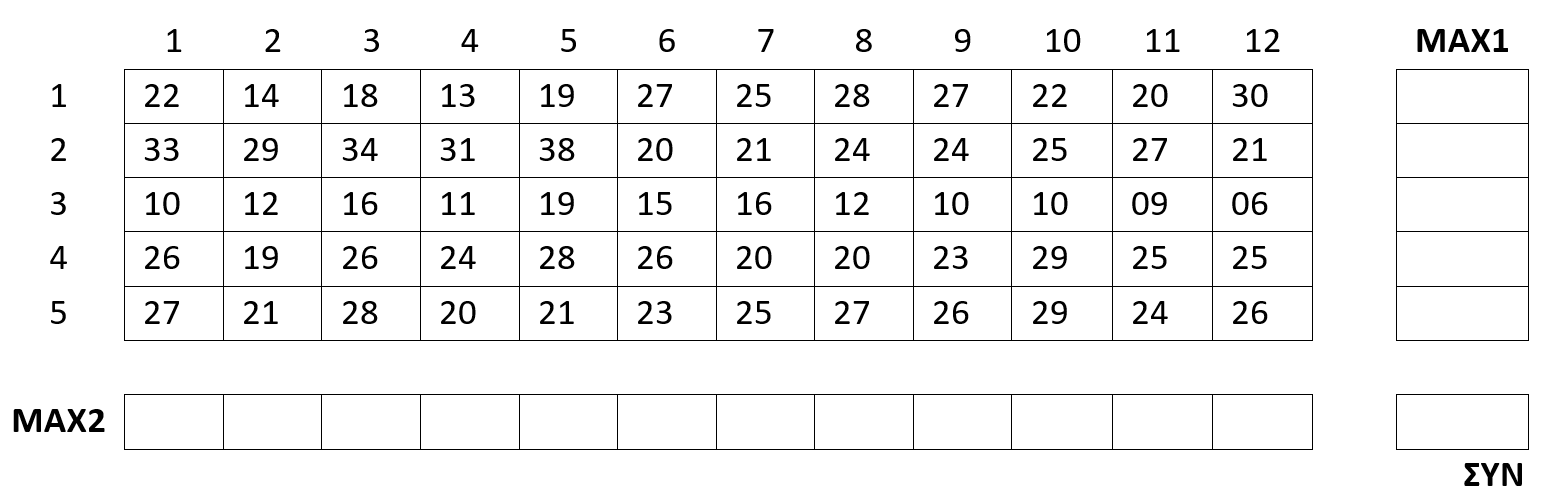
ΓΙΑ I ΑΠΟ 1 ΜΕΧΡΙ 5
ΜΑΧ1[i] ← 0
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΓΙΑ J ΑΠΟ 1 ΜΕΧΡΙ 12
ΜΑΧ2[j] ← 0
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΓΙΑ i ΑΠΟ 1 ΜΕΧΡΙ 5
ΓΙΑ j ΑΠΟ 1 ΜΕΧΡΙ 12
ΑΝ ΜΑΧ1[i]<Π[i,j] ΤΟΤΕ
ΜΑΧ1 [i] ← Π[i,j]
ΤΕΛΟΣ_ΑΝ
ΑΝ ΜΑΧ2[j]<Π[i,j] ΤΟΤΕ
ΜΑΧ2 [j] ← Π[i,j]
ΤΕΛΟΣ_ΑΝ
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
Ταξινόμηση των στοιχείων του πίνακα.
- Ταξινόμηση ευθείας ανταλλαγής (φυσαλίδας)
- Ταξινόμηση με επιλογή (selection sort)
- Στα κελιά 1 έως 100 αναζητούμε και βρίσκουμε το κελί με την μικρότερη τιμή και ανταλλάσσουμε την τιμή του με αυτή του πρώτου κελιού.
- Στα κελιά 2 έως 100 αναζητούμε και βρίσκουμε το κελί με την μικρότερη τιμή και ανταλλάσσουμε την τιμή του με αυτή του δεύτερου κελιού.
- Επαναλαμβάνουμε την διαδικασία μέχρι να φτάσουμε να αναζητούμε το μικρότερο στα κελιά 99 έως 100.
ΓΙΑ i ΑΠΟ 1 ΜΕΧΡΙ 99
min ←Π[i]
θέση ←i
ΓΙΑ j ΑΠΟ i+1 ΜΕΧΡΙ 100
ΑΝ Π[j] < min ΤΟΤΕ
min ←Π[j]
θέση ←j
ΤΕΛΟΣ_ΑΝ
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
Π[θέση] ← Π[i]
Π[i] ← min
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
Αν θέλουμε η ταξινόμηση να γίνει κατά φθίνουσα σειρά, αρκεί να αλλάξουμε την φορά της ανισότητας και φυσικά το όνομα της μεταβλητής min.
Παραλλαγές ταξινόμησης
Υπάρχουν ασκήσεις όπου οι παραπάνω μέθοδοι ταξινόμησης πρέπει να τροποποιηθούν:
- Ταξινόμηση αριθμών με βάση το πώς θα ήταν αν τους μετασχηματίζαμε σύμφωνα με μία σχέση. (Άσκηση 41)
- Ταξινόμηση αριθμών που βρίσκονται π.χ. στα μονά κελιά ενός πίνακα (1ο, 2ο, 3ο κλπ)
- Εύρεση των ν μεγαλύτερων αριθμών σε πίνακα με ταξινόμηση τμήματος αυτού του πίνακα.
- Ταξινόμηση πίνακα Π[Ν,2] ως προς μία στήλη και σε περίπτωση δύο κελιών με την ίδια τιμή τότε ταξινόμηση ως προς την άλλη στήλη. (Άσκηση 52)
- Ταξινόμηση που τερματίζεται μόλις διαπιστωθεί ότι ο πίνακας είναι πια ταξινομημένος.
Αναζήτηση
Αν και υπάρχουν αρκετοί αλγόριθμοι αναζήτησης ενός στοιχείου σε πίνακα, στην ύλη του μαθήματος συμπεριλαμβάνονται μόνο δύο :
- Γραμμική ή Σειριακή (linear ή sequential). Η πιο απλή περίπτωση, προσπελαύνουμε το πρώτο στοιχείο, μετά το δεύτερο κοκ μέχρι να βρούμε αυτό που αναζητούμε ή να τελειώσουν τα στοιχεία. Πρέπει να χρησιμοποιείται όταν:
- ο πίνακας είναι μη ταξινομημένος
- μικρού μεγέθους(<21) και
- η αναζήτηση στον πίνακα γίνεται σπάνια. (παράγραφος 3.6 σχολ. βιβλίου)
- Δυαδική (Binary). Στη δυαδική αναζήτηση η δομή δεδομένων χωρίζεται σε τρία τμήματα, στο στοιχείο της μεσαίας θέσης, στο τμήμα των στοιχείων που προηγούνται του μεσαίου και στο τμήμα των στοιχείων που έπονται του μεσαίου. Επειδή η δομή είναι ταξινομημένη, η σύγκριση του στοιχείου-κλειδιού με το μεσαίο θα δείξει σε ποιό τμήμα ανήκει το στοιχείο-κλειδί. Αν ισούται με το μεσαίο, τότε η αναζήτηση έληξε, αλλιώς ανάλογα με το είδος της ταξινόμησης (αύξουσα ή φθίνουσα) ο αλγόριθμος καλείται αναδρομικά για ένα από τα άλλα δύο τμήματα.
Αλγόριθμοι Γραμμικής/Σειριακής Αναζήτησης
Αλγόριθμος Sequential_Search_all_cells_unsorted
Δεδομένα // n, Π, key //flag ←ψευδής
Για i από 1 μέχρι 100
Αν (Π[i] = key) τότε
flag ←αληθής
Εκτύπωσε "Υπάρχει στο κελί:”, i
Τέλος_αν
Τέλος_επανάληψης
Αν (flag=ψευδής) τότε
Εκτύπωσε "Δεν βρέθηκε!"
Τέλος_Αν
Τέλος Sequential_Search_all_cells_unsorted
Περίπτωση 2 (του βιβλίου): Αναζήτηση στοιχείου σε μη ταξινομημένο πίνακα. Το στοιχείο μπορεί να βρίσκεται το πολύ σε ένα κελί.
Αλγόριθμος Sequential_Search_unsorted
Δεδομένα // 100, Π, key //
flag ← ψευδής
pos ← 0
i ← 1
Όσο (flag = ψευδής) και (i <= 100) επανάλαβε
Αν (Π[i] = key) τότε
flag ← αληθής
pos ← i
Αλλιώς
i ← i + 1
Τέλος_αν
Τέλος_επανάληψης
Αν (flag = αληθής) τότε
Εκτύπωσε "Το στοιχείο ", key, " ευρέθη στη θέση ", pos
Αλλιώς
Εκτύπωσε "Το στοιχείο ", key, " δεν ευρέθη στον δοθέντα πίνακα"
Τέλος_αν
Αποτελέσματα // flag , pos //
Τέλος Sequential_Search_ unsorted
Περίπτωση 3: Αναζήτηση στοιχείου σε ταξινομημένο πίνακα. Το στοιχείο μπορεί να βρίσκεται το πολύ σε ένα κελί.. Έστω ότι ο πίνακας είναι ταξινομημένος κατά αύξουσα σειρά.
Αλγόριθμος Sequential_Search_Sorted
Δεδομένα // 100, Π, key //
flag ← ψευδής
pos ← 0
i ← 1
Όσο (flag = ψευδής) και (i <= 100) επανάλαβε Αν (Π[i] > key) τότε
flag ← αληθής
Αλλιώς_Αν (Π[i] = key) τότε
flag ← αληθής
pos ← i
Αλλιώς
i ← i + 1
Τέλος_αν
Τέλος_επανάληψης
Αν (pos <> 0) τότε
Εκτύπωσε pos
Αλλιώς
Εκτύπωσε "Δεν βρέθηκε!"
Τέλος_αν
Αποτελέσματα // pos //
Τέλος Sequential_Search_Sorted
Περίπτωση 4: Αναζήτηση στοιχείου σε ταξινομημένο πίνακα. Το στοιχείο μπορεί να βρίσκεται σε περισσότερα του ενός κελιά. Έστω ότι ο πίνακας είναι ταξινομημένος κατά αύξουσα σειρά.
Αλγόριθμος Sequential_Search_Sorted
Δεδομένα // 100, Π, key //
flag ← ψευδής
pos ← 0
i ← 1
Όσο (flag = ψευδής) και (i <= 100) επανάλαβε
Αν (Π[i] > key) τότε
flag ← αληθής
Αλλιώς_Αν (Π[i] = key) τότε
Εκτύπωσε pos
pos ← i
i ← i + 1
Αλλιώς
i ← i + 1
Τέλος_αν
Τέλος_επανάληψης
Αν (pos = 0) τότε
Εκτύπωσε "Δεν βρέθηκε!"
Τέλος_αν
Αποτελέσματα // pos //
Τέλος Sequential_Search_Sorted
Αλγόριθμος Δυαδικής Αναζήτησης
Αλγόριθμος Δυαδική_Αναζήτηση1
Δεδομένα // 100, Π, key //
αρχή ← 1
τέλος ← 100
Μέση ← (αρχή + τέλος) div 2
Όσο αρχή <= τέλος και Π[μέση] <> Key επανάλαβε
Aν Key < Π[μέση] τότε
Τέλος ← μέση-1
αλλιώς
Αρχή ← μέση + 1
τελος_αν
Μέση ← (αρχή + τέλος) div 2
τελος _επανάληψης
Αν Π[μέση] = Key ΤΟΤΕ
γράψε 'Βρέθηκε στη θέση ',μέση
αλλιώς
γράψε 'Δεν βρέθηκε'
τέλος _αν
Τέλος Δυαδική_Αναζήτηση1
Αν ο πίνακας είναι ταξινομημένος κατά φθίνουσα σειρά τότε αρκεί να αλλάξουμε την ανισότητα στην εντολή: αν Key < Π[μέση] τότε. Δηλαδή να γίνει αν Key > Π[μέση] τότε Συγχώνευση δύο πινάκων.
Δυστυχώς η συγχώνευση αλλιώς ορίζεται στο κεφάλαιο 3.2 του βιβλίου και αλλιώς στο κεφάλαιο 9.4.
- «Συγχώνευση: η λειτουργία κατά την οποία δυο ή περισσότερες δομές συνενώνονται σε μια ενιαία δομή» (σελίδα 56).
- «Σκοπός της συγχώνευση είναι η δημιουργία από τα στοιχεία δυο ή περισσοτέρων ταξινομημένων πινάκων ενός άλλου, που είναι και αυτός ταξινομημένος» (σελίδα 166).
Προσοχή: Η συνένωση πινάκων ΔΕΝ είναι εφικτή στην ΓΛΩΣΣΑ!
Ερωτήσεις ανάπτυξης απο Πανελλαδικές εξετάσεις
- (2003-Θ1Γ) Να αναφέρετε τέσσερις τυπικές επεξεργασίες που γίνονται στα στοιχεία των πινάκων.
- (ΠΕ2016-Α2) Να αναφέρετε ονομαστικά τις τυπικές επεξεργασίες πινάκων.
- (2019-Α2, Β2019-Α2) Να αναφέρετε και να περιγράψετε τέσσερις από τις βασικές λειτουργίες επί των δομών δεδομένων που μπορούν να χρησιμοποιηθούν στους πίνακες.
- Δίνεται ο πίνακας Α (σχήμα 1) και το παρακάτω τμήμα προγράμματος:
sum ← 0 ΓΙΑ i ΑΠΟ 1 ΜΕΧΡΙ 5 ΓΙΑ j ΑΠΟ 1 ΜΕΧΡΙ 5 ΑΝ i = j ΤΟΤΕ sum ← sum + A[i,j] ΑΛΛΙΩΣ A[i,j] ← 0 ΤΕΛΟΣ_ΑΝ ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ ΓΡΑΨΕ sumΑυτό το τμήμα προγράμματος χρησιμοποιεί τον πίνακα Α, με τις τιμές των στοιχείων του, όπως αυτές φαίνονται στο σχήμα 1.
Σχήμα 1: Πίνακας Α1 -1 7 1 1 6 2 0 8 -2 4 9 3 3 0 3 5 -4 2 1 0 1 2 0 1 - Να σχεδιάσετε στο τετράδιο σας τον πίνακα Α με τις τιμές που θα έχουν τα στοιχεία του, μετά την εκτέλεση του τμήματος προγράμματος.
- (Β2003-Θ2) Ποια είναι η τιμή της μεταβλητής sum που θα εμφανιστεί;
- (2020 A2 Νέο) Να αναφέρετε τις τυπικές επεξεργασίες των πινάκων.
- x
- x