Δένδρα (ή Δέντρα)
Μέχρι τώρα όλες οι δομές δεδομένων που προηγήθηκαν ήταν γραμμικές. Τι σημαίνει αυτό; Σημαίνει οτι τα στοιχεία τους είχαν μια σειρά. Δηλαδή κάποιο ήταν πρώτο, κάποιο άλλο δεύτερο κλπ.. Στα δένδρα όπως θα δούμε στην συνέχεια δεν ισχύει κάτι τέτοιο. Μετά από ένα στοιχείο μπορούν να ακολουθούν πολλά στοιχεία χωρίς κάποιο να προηγείται. Τα δένδρα μοιάζουν με τα γενεολογικά δένδρα ή με τα διαγράμματα που δείχνουν την ιεραρχία σε μία εταιρία.
Τι ονομάζουμε δένδρο;
Ένα δένδρο (tree) είναι μία δομή δεδομένων που αποτελείται από ένα σύνολο κόμβων και ένα σύνολο ακμών (βέλη) μεταξύ των κόμβων με βάση τους εξής κανόνες:
• Υπάρχει ένας ξεχωριστός κόμβος που ονομάζεται ρίζα. Αυτός είναι ένας κόμβος χωρίς γονέα.
• Για κάθε κόμβο c, εκτός από τη ρίζα, υπάρχει μόνο μια ακμή που καταλήγει στον κόμβο αυτόν ξεκινώντας από κάποιον άλλον κόμβο p. Ο κόμβος p ονομάζεται γονέας του c και ο κόμβος c παιδί του p.
• Για κάθε κόμβο υπάρχει μία μοναδική διαδρομή, δηλαδή, μια ακολουθία διαδοχικών ακμών, που ξεκινάει από τη ρίζα και τερματίζει σε αυτόν τον κόμβο.
Προσοχή! Οι δύο τελευταίες περιπτώσεις είναι ισοδύναμες. Παρόλα αυτά στις εξετάσεις θα πρέπει να τις αναφέρετε και τις δύο.
Δένδρο θεωρούμε και το κενό δένδρο, δηλαδή το δένδρο που δεν έχει ούτε κόμβους, ούτε ακμές. Το κενό δένδρο είναι το μόνο δένδρο χωρίς ρίζα.
Γιατί ονομάζονται δένδρα;
Για να δείτε πως προέκυψε το όνομα Δένδρο πατήστε το κουμπί που ακολουθεί.
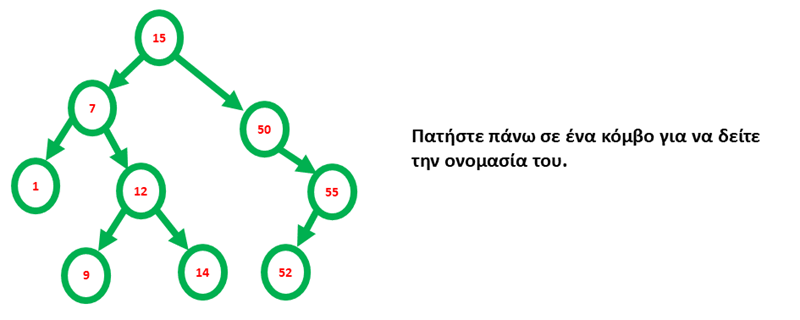
Ονομασίες σε ένα δένδρο
Δομές Δεδομένων που δεν είναι Δένδρα
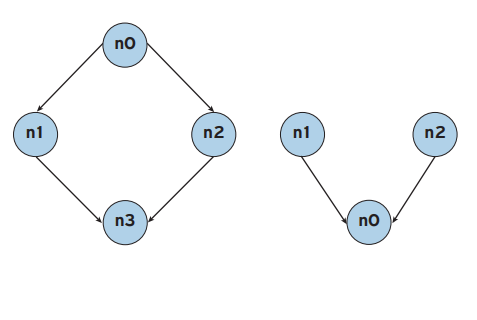
Στην πρώτη εικόνα (αριστερά) παρατηρούμε οτι υπάρχουν 2 διαδρομές από τον κόμβο n0 στον n3. Αντίστοιχα στην δεύτερη παρατηρούμε οτι έχει 2 ρίζες.
Υποδένδρο
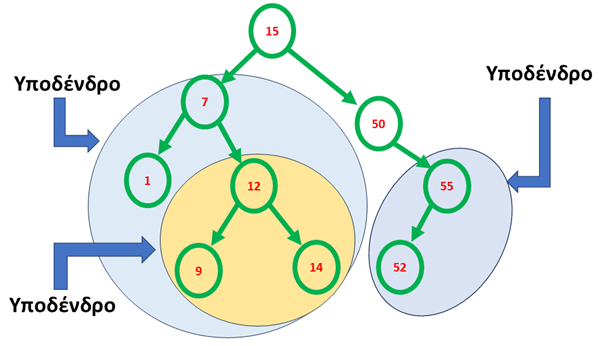
Υποδένδρο ονομάζουμε ένα τμήμα από δένδρο που είναι και αυτό δένδρο. Αν απομονώσουμε έναν οποιοδήποτε κόμβο μαζί με τους απογόνους του τότε έχουμε ένα υποδένδρο.
Διατεταγμένο Δένδρο.
Έτσι ονομάζονται τα δένδρα στα οποία τα παιδιά ενός οποιουδήποτε κόμβου είναι ταξινομημένα (όχι κατά ανάγκη κατά αύξουσα ή φθίνουσα σειρά). Για παράδειγμα, σε ένα δένδρο με ονόματα υπαλλήλων θα μπορούσαν τα παιδιά κάθε κόμβου να μπάινουν με βάση το φύλλο (π.χ. πρώτα οι γυναίκες και μετά οι άνδρες).
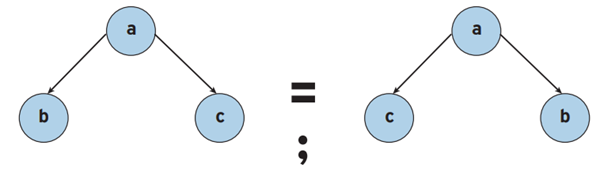
Το σχολικό βιβλίο έχει μία ενδιαφέρουσα ερώτηση παγίδα: Τα παρακάτω δένδρα είναι ίδια ή όχι; Η απάντηση είναι εξαρτάται. Αν είναι διατεταγμένα τότε ΟΧΙ αλλιώς ΝΑΙ.
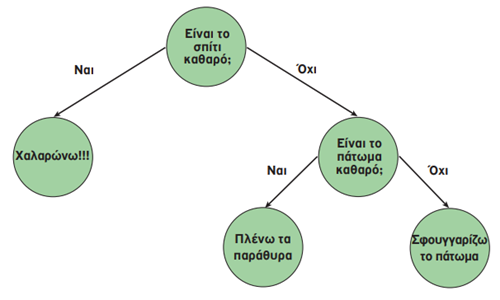
Δένδρο απόφασης.
Πρόκειται για δένδρα που μας βοηθάνε να καταλήξουμε σε ένα συμπέρασμα (να πάρουμε απόφαση). Κάθε κόμβος περιέχει μία ερώτηση και κάθε ακμή του αντιστοιχεί σε μία πιθανή απάντηση. Κάθε φύλλο αντιπροσωπεύει μια πρόβλεψη της
λύσης στο πρόβλημα που εξετάζεται.
Δυαδικό δένδρο (binary tree).
Πρόκειται για δένδρα με τα εξής δύο χαρακτηριστικά:
- Είναι διατεταγμένα.
- Κάθε κόμβος έχει το πολύ δύο παιδιά (0-2).
Δένδρα αναπαράστασης αριθμητικών εκφράσεων
Πρόκειται για δένδρα που αναπαριστούν αριθμητικές εκφράσεις π.χ. 3 + ((5+9)*2). Πατήστε το ακόλουθο κουμπί για να δείτε την διαδικασία κατασκευής ενός τέτοιου δένδρου.
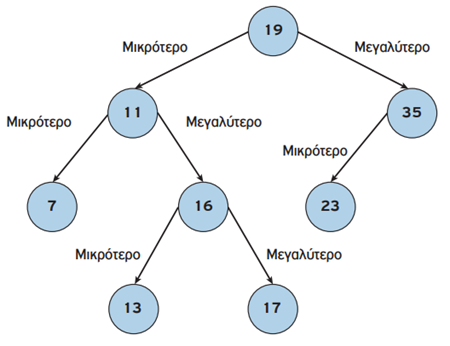
Δυαδικό δένδρο αναζήτησης (binary search tree).
Πρόκειται για δένδρα με τα εξής δύο χαρακτηριστικά:
- Είναι δυαδικά
- για κάθε κόμβο Α, όλοι οι κόμβοι του αριστερού υποδένδρου έχουν τιμές μικρότερες της τιμής του κόμβου Α και όλοι
οι κόμβοι του δεξιού υποδένδρου έχουν τιμές μεγαλύτερες (ή ίσες) της τιμής του κόμβου Α.
Δένδρο του παιχνιδιού (game tree).
Τέτοια δένδρα συναντάμε σε παιχνίδια στον υπολογιστή, όπως είναι το σκάκι, η τρίλιζα, το τάβλι και πολλά άλλα. Ο υπολογιστής χρησιμοποιεί ένα ειδικό δένδρο, που ονομάζεται δένδρο του παιχνιδιού (game tree), το οποίο μοντελοποιεί όλες τις πιθανές κινήσεις των παικτών. Κάθε κόμβος στο δένδρο, αντιπροσωπεύει μία συγκεκριμένη κατάσταση του παιχνιδιού και περιέχει πληροφορίες σχετικά με το ποιος παίκτης έχει τη μεγαλύτερη πιθανότητα να κερδίσει. Αυτό βοηθάει τον υπολογιστή να διαλέξει την βέλτιστη επόμενη κίνηση του.
Ισορροπημένο δένδρο.
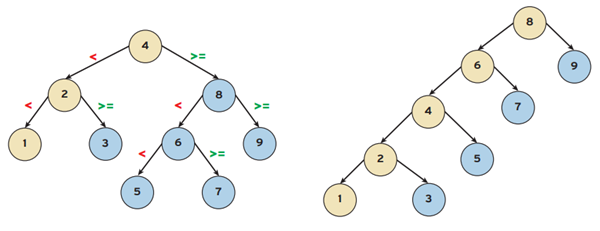
Ένα δένδρο λέγεται ισορροπημένο όταν για κάθε κόμβο το πλήθος των κόμβων που είναι αριστερά του και αυτών που είναι δεξιά του είναι σχεδόν το ίδιο. Αν παρατηρήσετε τα ακόλουθα δύο δένδρα θα δείτε ότι αυτό στα αριστερά είναι πιο ισορροπημένο.
Στα ισορροπημένα δένδρα η αναζήτηση μιας τιμής είναι σημαντικά ταχύτερη.