- (B2008-Θ2Α) Δίνεται το παρακάτω τμήμα αλγορίθμου:
X ← 2
ΑΡΧΗ_ΕΠΑΝΑΛΗΨΗΣ
ΑΝ X MOD 4 > 2 ΤΟΤΕ
X ← X + 2
ΑΛΛΙΩΣ
X ← X + 3
ΤΕΛΟΣ_ΑΝ
ΕΜΦΑΝΙΣΕ X
ΜΕΧΡΙΣ_ΟΤΟΥ X > 15
α. Ποιο είναι το πλήθος των επαναλήψεων που θα εκτελεστούν;
β. Να γράψετε στο τετράδιό σας την τιμή της μεταβλητής X που θα εμφανιστεί σε κάθε επανάληψη.
γ. Ποια είναι η τελική τιμή της μεταβλητής X;
- (E2004-Θ2) Δίνεται ο παρακάτω αλγόριθμος:
Αλγόριθμος Αριθμοί_ΜΕΡΣΕΝ
Διάβασε Α
B ← 4
C ← 2
Αρχή_επανάληψης
B ← (B^2) - 2
Εμφάνισε B
C ← C + 1
Μέχρις_ότου C > (A - 1)
D ← (2^A) - 1
E ← B MOD D
Εμφάνισε D
Αν E = 0 τότε
F ← (2^ (C - 1)) * D
Εμφάνισε "Τέλειος αριθμός:", F
G ← 0
Όσο F > 0 επανάλαβε
G ← G + 1
F ← F DIV 10
Τέλος_επανάληψης
Εμφάνισε G
Τέλος_αν
Τέλος Αριθμοί_ΜΕΡΣΕΝ
Να γράψετε στο τετράδιό σας τις τιμές που τυπώνει ο παραπάνω αλγόριθμος, αν του δώσουμε τιμές εισόδου:
α. 3
β. 4
- (2010-B) Δίνεται το παρακάτω τμήμα αλγορίθμου, στο οποίο έχουν αριθμηθεί οι γραμμές:
1 j ← 1
2 i ← 2
3 Αρχή_επανάληψης
4 i ← i + j
5 j ← i - j
6 Εμφάνισε i
7 Μέχρις_ότου i ≥ 5
Επίσης δίνεται το ακόλουθο υπόδειγμα πίνακα τιμών:
| αριθμός γραμμής |
συνθήκη |
έξοδος |
i |
j |
|
|
|
|
|
Στη στήλη με τίτλο «αριθμός γραμμής» καταγράφεται ο αριθμός γραμμής της εντολής που εκτελείται.
Στη στήλη με τίτλο «συνθήκη» καταγράφεται η λογική τιμή ΑΛΗΘΗΣ ή ΨΕΥΔΗΣ, εφόσον η εντολή που εκτελείται περιλαμβάνει συνθήκη.
Στη στήλη με τίτλο «έξοδος» καταγράφεται η τιμή εξόδου, εφόσον η εντολή που εκτελείται είναι εντολή εξόδου.
Στη συνέχεια του πίνακα υπάρχει μια στήλη για κάθε μεταβλητή του αλγορίθμου.
Να μεταφέρετε τον πίνακα στο τετράδιό σας και να τον συμπληρώσετε εκτελώντας τις εντολές του τμήματος αλγορίθμου ως εξής:
Για κάθε εντολή που εκτελείται να γράψετε σε νέα γραμμή του πίνακα τον αριθμό της γραμμής της και το αποτέλεσμα της στην αντίστοιχη στήλη.
Σημείωση: Η εντολή της γραμμής 3 δεν χρειάζεται να αποτυπωθεί στον πίνακα.
- (2014-Α5, Β2014-Α5) Δίδεται το παρακάτω ημιτελές τμήμα αλγορίθμου:
Α ← …
Β ← …
Αρχή_επανάληψης
Β ← …
Α ← …
Μέχρις_ότου Α>200
Εμφάνισε Β
Να ξαναγράψετε στο τετράδιό σας το παραπάνω τμήμα αλγορίθμου με τα κενά συμπληρωμένα, έτσι ώστε να υπολογίζει και να εμφανίζει το άθροισμα των περιττών ακεραίων από το 100 έως το 200.
- (EB2004-Θ1Β-2) Δίνεται η παρακάτω δομή επανάληψης:
Α ← 10
Β ← 20
ΑΡΧΗ_ΕΠΑΝΑΛΗΨΗΣ
Β ← Β + Α
ΓΡΑΨΕ Α, Β
ΜΕΧΡΙΣ_ΟΤΟΥ Β > 50
α. «Οι εντολές που περιέχονται στη δομή επανάληψης εκτελούνται τρεις (3) φορές». Να γράψετε στο τετράδιό σας αν η παραπάνω πρόταση είναι σωστή ή λανθασμένη.
β. Να δικαιολογήσετε την απάντησή σας.
- (E2001-Θ1Ε) Αντιστοιχίστε σωστά τις εκφράσεις στη Στήλη Α με τις αλγοριθμικές έννοιες της Στήλης Β, γράφοντας στο τετράδιό σας τους αριθμούς της Στήλης Α και δίπλα το γράμμα της Στήλης Β.
| Στήλη Α
Εκφράσεις |
Στήλη Β
Εκφράσεις |
| 1. X <- X * 2 |
α. αριθμητική έκφραση (παράσταση) |
| 2. 3 + A > B |
β. μεταβλητή |
| 3. τύπωσε Β |
γ. λογική έκφραση (παράσταση) |
| 4. όσο Κ<3 επανάλαβε εντολές |
δ. δομή ακολουθίας |
| τέλος_επανάληψης |
ε. δομή επανάληψης |
| 5. X – (X/2) * 2 |
στ. εντολή εκχώρησης |
|
ζ. εντολή εξόδου |
- (E2003-Θ2) ∆ίνεται ο παρακάτω αλγόριθµος :
Αλγόριθµος Αριθµοί
∆ιάβασε Α
Εκτύπωσε Α
S ← 1
K ← 2
Αρχή_επανάληψης
Αν Α MOD K = 0 τότε
Β ← Α DIV K
Αν Κ <> Β τότε
S ← S + K + B
Εκτύπωσε Κ, Β
αλλιώς
S ← S + K
Εκτύπωσε Κ
Τέλος_αν
Τέλος_αν
Κ ← Κ + 1
Μέχρις_ότου Κ > Ρίζα (Α)
Αν Α = S τότε
Εκτύπωσε S
Τέλος_αν
Τέλος Αριθµοί
Η συνάρτηση Ρίζα (Α) επιστρέφει την τετραγωνική ρίζα του Α.
Να γράψετε στο τετράδιό σας τις τιµές που τυπώνει ο παραπάνω αλγόριθµος, αν του δώσουµε τιµές εισόδου :
α. 36
β. 28
- (2018-Α3, Β2018-Α3) Σε ένα πρόγραμμα επιλογής υποψηφίων απαιτείται η είσοδος τριών τιμών από τον χρήστη για τις οποίες ισχύουν οι εξής περιορισμοί:
- ηλικία: από 18 έως και 21
- φύλο: ένα από τα γράμματα Α (για τους άνδρες), Θ (για τις γυναίκες)
- ύψος: πάνω από 1,70 για τους άνδρες και πάνω από 1,60 για τις γυναίκες.
Δίδεται το παρακάτω τμήμα αλγορίθμου το οποίο υλοποιεί τους συγκεκριμένους περιορισμούς. Το τμήμα αυτό περιέχει κενά που έχουν αριθμηθεί. Να γράψετε στο τετράδιό σας τους αριθμούς των κενών και δίπλα σε κάθε αριθμό τη συνθήκη που αντιστοιχεί.
Αρχή_επανάληψης
Διάβασε ηλικία
Μέχρις_ότου ...(1)...
Αρχή_επανάληψης
Διάβασε φύλο
Μέχρις_ότου ...(2)...
Αρχή_επανάληψης
Διάβασε ύψος
Μέχρις_ότου ...(3)...
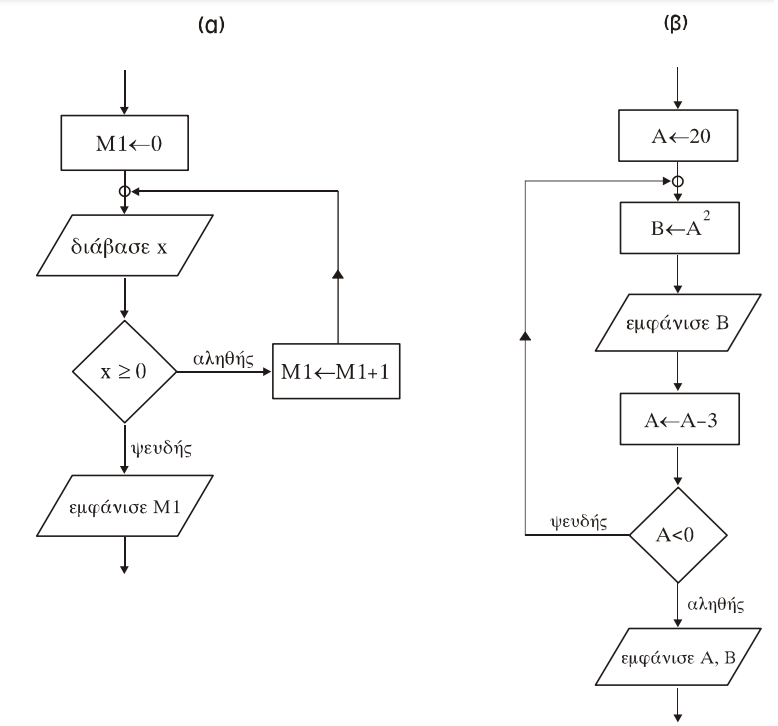
- (Β2002-Θ1Δ) Να γράψετε τα τμήματα αλγορίθμου, που αντιστοιχούν στα τμήματα των διαγραμμάτων ροής (α) και (β), που ακολουθούν.
- (2011-Θ Α3) Δίδεται το παρακάτω τμήμα αλγορίθμου:
Δ ← Αληθής
Για α από 1 μέχρι Ν
Δ ← ΟΧΙ Δ
Τέλος_επανάληψης
Εμφάνισε Δ
Να το εκτελέσετε για καθεμία από τις παρακάτω περιπτώσεις:
1. Ν=0
2. Ν=1
3. Ν=4
4. Ν=2011
5. Ν=8128
και να γράψετε στο τετράδιό σας τον αριθμό καθεμίας από τις παραπάνω περιπτώσεις 1-5 και δίπλα τη λογική τιμή που θα εμφανιστεί μετά την εκτέλεση της αντίστοιχης περίπτωσης.
- (2014-B2, Β2014-B1) Δίδεται ο παρακάτω αλγόριθμος:
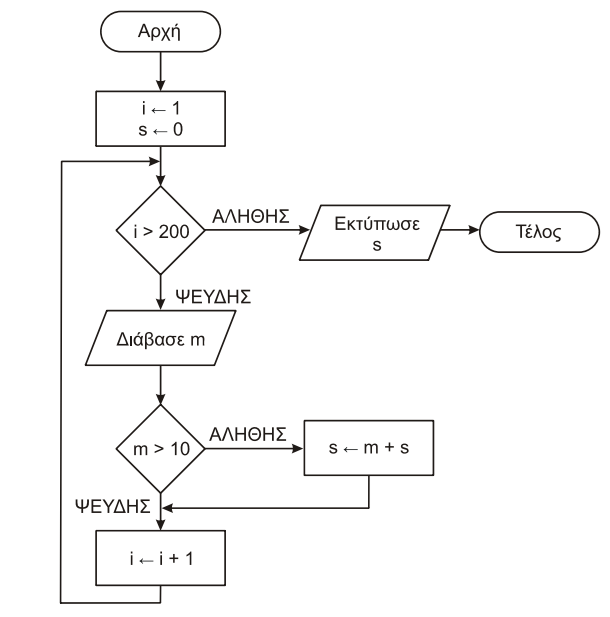Να κωδικοποιήσετε τον παραπάνω αλγόριθμο σε ψευδογλώσσα.
- (E2011-Θ Α4, ΕΒ2011-Θ Α4) Δίδεται το παρακάτω τμήμα αλγορίθμου:
Για Χ από Α μέχρι Μ με_βήμα Β
Εμφάνισε Χ
Τέλος_επανάληψης
Να γράψετε στο τετράδιό σας για καθεμία από τις παρακάτω περιπτώσεις τις τιμές των A, M, B, έτσι ώστε το αντίστοιχο τμήμα αλγορίθμου να εμφανίζει όλους:
1. τους ακέραιους από 1 μέχρι και 100
2. τους ακέραιους από 10 μέχρι και 200 σε φθίνουσα σειρά
3. τους ακέραιους από -1 μέχρι και -200 σε αύξουσα σειρά
4. τους άρτιους ακέραιους από 100 μέχρι και 200
5. τους θετικούς ακέραιους που είναι μικρότεροι του 8128 και πολλαπλάσια του 13.
- (2015-ΘΒ1, 2015-ΘΒ2) Δίδεται το παρακάτω τμήμα αλγορίθμου, όπου η μεταβλητή x έχει θετική ακέραια τιμή:
Αν x>1 τότε
y←x
Αρχή_επανάληψης
y←y-2
Εμφάνισε y
Μέχρις_ότου y≤0
Τέλος_αν
α. Να σχεδιάσετε στο τετράδιό σας το ισοδύναμο διάγραμμα ροής.
β. Να ξαναγράψετε το τμήμα αυτό στο τετράδιό σας, χρησιμοποιώντας την εντολή Για αντί της εντολής Μέχρις_ότου.
- (2011-Θ Α2, Β2011-Θ Α2) Δίδεται το παρακάτω τμήμα αλγορίθμου με αριθμημένες τις εντολές του:
(1) Σ ← 0
(2) Κ ← 0
(3) Αρχή_Επανάληψης
(4) Διάβασε Χ
(5) Σ ← Σ+Χ
(6) Αν Χ ≥ 0 τότε
(7) Κ ← Κ+1
(8) Τέλος_Αν
(9) Μέχρις_ότου Σ > 1000
(10) Εμφάνισε Χ
Να γράψετε στο τετράδιό σας τον αριθμό καθενιάς από τις παρακάτω προτάσεις 1-5 και δίπλα τη λέξη ΣΩΣΤΟ, αν είναι σωστή, ή τη λέξη ΛΑΘΟΣ, αν είναι λανθασμένη.
1. Η εντολή (4) θα εκτελεστεί τουλάχιστον μία φορά.
2. Η εντολή (1) θα εκτελεστεί ακριβώς μία φορά.
3. Στη μεταβλητή Κ καταχωρείται το πλήθος των θετικών αριθμών που δόθηκαν.
4. Η εντολή (7) εκτελείται πάντα λιγότερες φορές από την εντολή (4).
5. Η τιμή που θα εμφανίσει η εντολή (10) μπορεί να είναι αρνητικός αριθμός.
6. Η εντολή (6) εκτελείται λιγότερες φορές από την εντολή (4).
- (EB2008-Θ2) Δίδεται το παρακάτω τμήμα αλγορίθμου:
Χ←0
Α←10
Β←14
ΟΣΟ Β>0 ΕΠΑΝΑΛΑΒΕ
ΑΝ Β MOD 2 = 0 ΤΟΤΕ
Χ←Χ+Α
ΤΕΛΟΣ_ΑΝ
Α←Α*2
Β←Β DIV 2
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
α. Να γράψετε στο τετράδιό σας τις τιμές των μεταβλητών Χ, Α και Β στο τέλος κάθε επανάληψης κατά την εκτέλεση του παραπάνω τμήματος αλγορίθμου.
β. Να σχεδιάσετε το αντίστοιχο διάγραμμα ροής.
- (B2010-A4) Δίδεται το παρακάτω τμήμα διαγράμματος ροής:
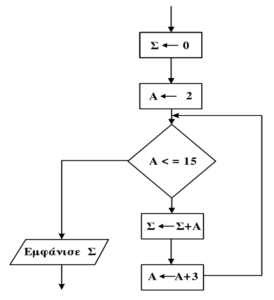Να μετατρέψετε σε ισοδύναμο τμήμα αλγορίθμου σε ψευδογλώσσα, χρησιμοποιώντας αποκλειστικά την εντολή επανάληψης Για … από …. Μέχρι …. Με_βήμα
- (2012-B2, B2012-B2) Δίνεται το παρακάτω τμήμα αλγορίθμου σε μορφή διαγράμματος ροής:
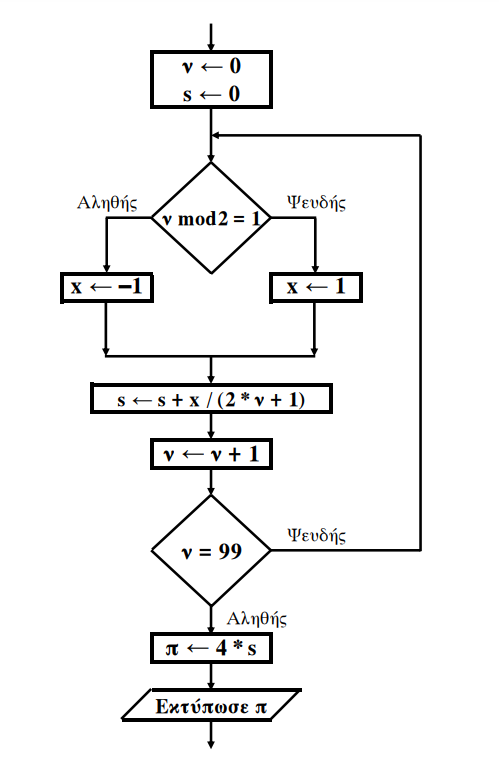Να κατασκευάσετε ισοδύναμο τμήμα αλγορίθμου σε ψευδογλώσσα.
- (B2011-Θ Β1) Δίνεται το παρακάτω αλγόριθμος:
Αλγόριθμος ΘέμαΒ
z ← 1
w ← 3
Όσο z ≤ 35 επανάλαβε
z ← z + w
w ← w + 2
Γράψε w, z
Τέλος_επανάληψης
Τέλος ΘέμαΒ
Να γράψετε στο τετράδιό σας τις τιμές που θα εμφανιστούν κατά την εκτέλεση του αλγόριθμου με τη σειρά που θα εμφανιστούν.
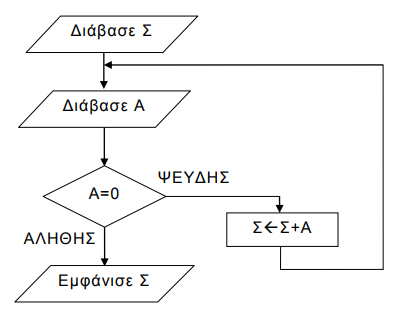
- (2018-B2) Δίνεται το παρακάτω τμήμα αλγορίθμου: Να κωδικοποιήσετε σε ΓΛΩΣΣΑ αντίστοιχο τμήμα προγράμματος που να εκτελεί ακριβώς την ίδια ακολουθία εντολών (βημάτων).
- (B2014-A5) Δίνεται το παρακάτω τμήμα αλγορίθμου:
z ← 3
Για i από 7 μέχρι 15
z ← z*i
Εμφάνισε z
Τέλος_επανάληψης
Να ξαναγράψετε στο τετράδιό σας το παραπάνω τμήμα αλγορίθμου χρησιμοποιώντας αποκλειστικά την εντολή επανάληψης Όσο…επανάλαβε.
- (B2013-A2) Στο παρακάτω τμήμα αλγορίθμου να αναφέρετε ποια αλγοριθμικά κριτήρια παραβιάζονται (μονάδες 3). Να αιτιολογήσετε την απάντησή σας (μονάδες 5).
1. N ← 0
2. M ← 4
3. Όσο M≤11 Επανάλαβε
4. Αν Μ mod 10=0 τότε
5. Μ ← Μ-4
6. Τέλος_αν
7. Μ ← Μ+2
8. N←Ν+2* Ν / (Μ-10)
9. Τέλος_επανάληψης
10. N ← (Ν-Μ)/Ν
11. Εμφάνισε Μ
12. Εμφάνισε Ν
- (2011-B1) Δίνεται το παρακάτω τμήμα αλγορίθμου σε μορφή διαγράμματος ροής:
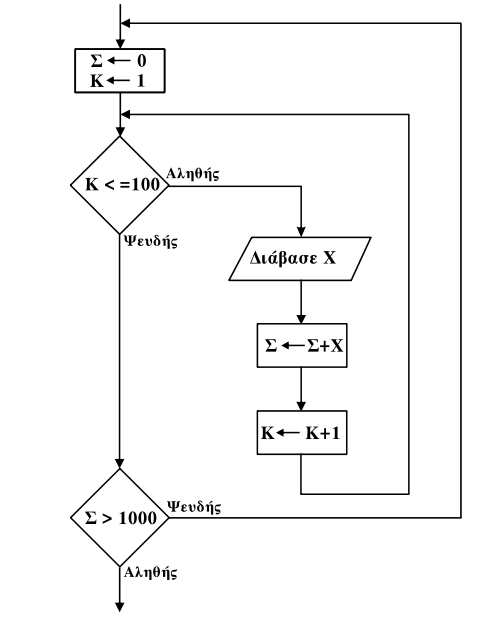Να κατασκευάσετε ισοδύναμο τμήμα αλγορίθμου σε ψευδογλώσσα.
- (E2012-B1, EB2012-B1) Δίνεται ο παρακάτω αλγόριθμος:
Αλγόριθμος Διοφαντική
Για x από 0 μέχρι 100
Για y από 0 μέχρι 100
Για z από 0 μέχρι 100
Αν 3*x + 2*y - 7*z = 5 τότε εκτύπωσε x, y, z
Τέλος_επανάληψης
Τέλος_επανάληψης
Τέλος_επανάληψης
Τέλος Διοφαντική
Να κατασκευάσετε το διάγραμμα ροής για τον παραπάνω αλγόριθμο.
- (B2011-Θ B1) Δίνεται το παρακάτω τμήμα αλγορίθμου:
Διάβασε Χ
Αν Χ >= 0 τότε
π ← 1
Για i από 1 μέχρι Χ
π ← π * i
Τέλος_επανάληψης
Εμφάνισε π
Αλλιώς
Εμφάνισε "Δεν υπάρχει παραγοντικό"
Τέλος_αν
Να κατασκευάσετε ισοδύναμο διάγραμμα ροής.
- (ΠΕ2016-B1) Δίνεται ο παρακάτω αλγόριθμος:
Αλγόριθμος θέμα_Β1
ΠΛ ← 0
Σ ← 0
Για Ι από 100 μέχρι 10 με_βήμα -3
Αν Ι mod 2 <> 0 τότε
Σ ← Σ + Ι
Αλλιώς
ΠΛ ← ΠΛ + 1
Τέλος_αν
Τέλος_επανάληψης
Εμφάνισε Σ, ΠΛ
Τέλος θέμα_Β1
Να σχεδιάσετε στο τετράδιό σας το αντίστοιχο διάγραμμα ροής.
- (Ε2011-Θ Β1, ΕΒ2011-Θ Β1) Δίνεται το παρακάτω τμήμα αλγορίθμου, το οποίο διαβάζει έναν θετικό αριθμό από τον χρήστη. Αν δοθεί μη θετικός αριθμός ζητάει από τον χρήστη άλλον αριθμό.
Αρχή_επανάληψης
Διάβασε α
Μέχρις_ότου α > 0
Να ξαναγράψετε στο τετράδιό σας τον παραπάνω αλγόριθμο τροποποιημένο, έτσι ώστε:
α. Να υπολογίζει και να εμφανίζει πόσες φορές δόθηκε μη θετικός αριθμός. Αν δοθεί την πρώτη φορά θετικός αριθμός να εμφανίζει το μήνυμα “Σωστά”.
β. Να υπολογίζει και να εμφανίζει τον μέσο όρο των μη θετικών αριθμών που δόθηκαν. Αν δεν δοθούν μη θετικοί αριθμοί να εμφανίζει κατάλληλο μήνυμα.
γ. Να υπολογίζει και να εμφανίζει τον μεγαλύτερο κατά απόλυτη τιμή μη θετικό αριθμό που δόθηκε. Αν δεν δοθούν μη θετικοί αριθμοί να εμφανίζει κατάλληλο μήνυμα.
- (Ε2011-Θ Α3, ΕΒ2011-Θ Α3) Να ξαναγράψετε στο τετράδιό σας καθένα από τα παρακάτω τμήματα αλγορίθμου, χρησιμοποιώντας μόνο μία δομή επανάληψης Για…Από…Μέχρι και χωρίς τη χρήση δομής επιλογής.
| (α) |
(β) |
| i ← 1
j ← 1
Αρχή_επανάληψης
Εμφάνισε Α[i,j]
i ← i + 1
j ← j + 1
Μέχρις_ότου j > 100 |
Για i από 1 μέχρι 100
Για j από 1 μέχρι 100
Αν i = 50 τότε
Εμφάνισε Α[i,j]
Τέλος_αν
Τέλος_επανάληψης
Τέλος_επανάληψης |
- (2003-Θ1Β) Να γράψετε στο τετράδιό σας τους αριθμούς της Στήλης Α και δίπλα τα γράμματα της Στήλης Β που αντιστοιχούν σωστά. (Να σημειωθεί ότι σε κάποια στοιχεία της ψευδογλώσσας της Στήλης Α αντιστοιχούν περισσότερα από ένα παραδείγματα εντολών της Στήλης Β).
| Α. Στοιχεία ψευδογλώσσας |
Β. Παραδείγματα εντολών |
| 1. εντολή εκχώρησης |
α. Επίλεξε Χ
Περίπτωση 1
Χ ← Χ + 1
Περίπτωση 2
Χ ← α * β
Τέλος_επανάληψης |
|
|
| 2. δομή επιλογής |
β. Όσο Χ < 0 επανάλαβε
Χ ← Χ – 1
Τέλος_επανάληψης |
| 3. δομή επανάληψης |
γ. α ← β + 1
δ. Αρχή_επανάληψης
Ι ← Ι-1
Μέχρις_ότου Ι<0
Ε. Αν Χ=2 τότε
Χ←Χ/2
Τέλος_αν |
- (2004-Θ1Β) Να γράψετε στο τετράδιό σας τους αριθμούς της Στήλης Α και δίπλα τα γράμματα της Στήλης Β που αντιστοιχούν σωστά. (Να σημειωθεί ότι στις Εντολές της Στήλης Α αντιστοιχούν περισσότερες από μία Προτάσεις της Στήλης Β).
| Α. Εντολές |
Β. Προτάσεις |
| 1. Όσο συνθήκη επανάλαβε εντολές Τέλος_επανάληψης |
α. Ο βρόχος επανάληψης τερματίζεται, όταν η συνθήκη είναι αληθής |
| 2. Αρχή επανάληψης εντολές Μέχρις_ότου συνθήκη |
β. Ο βρόχος επανάληψης τερματίζεται, όταν η συνθήκη είναι ψευδής |
|
γ. Ο βρόχος επανάληψης εκτελείται οπωσδήποτε μία φορά |
|
δ. Ο βρόχος επανάληψης είναι δυνατόν να μην εκτελεστεί |
- (E2001-Θ1Δ) Δίνεται το παρακάτω τμήμα αλγορίθμου:
X <- A
Αρχή_επανάληψης
X <- X + 2
Τύπωσε το X
Μέχρις_ότου X >= M
a. Να δώσετε τη δομή επανάληψης «Για … από … μέχρι … βήμα» η οποία τυπώνει ακριβώς τις ίδιες τιμές με το πιο πάνω τμήμα αλγορίθμου.
b. Τι θα τυπωθεί, αν A=4 και M=9;
c. Τι θα τυπωθεί, αν A=-5 και M=0;
- (E2004-Θ1Δ) Δίνεται η παρακάτω αλληλουχία εντολών:
Α ← x
Όσο Α < = y επανάλαβε
Α ← Α + z
Τέλος_επανάληψης
Να γράψετε στο τετράδιο σας πόσες φορές εκτελείται η εντολή Α ← Α + z για κάθε έναν από τους παρακάτω συνδυασμούς των τιμών των μεταβλητών x, y και z:
1. x = 0 y = 8 z = 3
2. x = 7 y = 10 z = 5
3. x = -10 y = -5 z = -1
4. x = 10 y = 5 z = 2
- (B2004-Θ1Γ) Δίνεται το παρακάτω τμήμα αλγορίθμου:Χ ← 50
ΟΣΟ Χ > 0 ΕΠΑΝΑΛΑΒΕ
ΓΙΑ Υ ΑΠΟ 2 ΜΕΧΡΙ 6 ΜΕ_ΒΗΜΑ 2
Χ ← Χ – 10
ΤΕΛΟΣ ΕΠΑΝΑΛΗΨΗΣ
ΓΡΑΨΕ Χ
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ1. Πόσες φορές θα εκτελεστεί η εντολή ΓΡΑΨΕ Χ;
2. Πόσες φορές θα εκτελεστεί η εντολή εκχώρησης Χ ← Χ – 10;
3. Ποιες είναι οι διαδοχικές τιμές των μεταβλητών Χ και Υ σε όλες τις επαναλήψεις;
- (EB2006-Θ2) Δίνεται το παρακάτω τμήμα αλγορίθμου:Διάβασε M
Για Χ από 3 μέχρι M-1 με_βήμα 2
Α ← 2*Χ + 4
Β ← 4*Χ – 3
Αν (Β – Α < 0) ή (Α > 15) τότε
Α ← Α + 5
Β ← Β * 2
Τέλος_αν
Εμφάνισε Α, Β
Τέλος_επανάληψηςΝα γράψετε στο τετράδιό σας τις τιμές των μεταβλητών Α και Β που εμφανίζονται κατά την εκτέλεση του παραπάνω τμήματος αλγορίθμου, όταν για M δώσουμε την τιμή 9.
- (B2007-Θ1Β) Δίνεται η παρακάτω εντολή:
Για Α από Β μέχρι Γ με_βήμα Δ
Εμφάνισε “ΚΑΛΗΣΠΕΡΑ”
Τέλος_επανάληψηςΝα γράψετε στο τετράδιό σας πόσες φορές εκτελείται η εντολή Εμφάνισε για καθένα από τους παρακάτω συνδυασμούς των τιμών των μεταβλητών Β, Γ και Δ:
1. Β = 2, Γ = 5, Δ = 1
2. Β = -1, Γ = 1, Δ = 0,5
3. Β = -7, Γ = -6, Δ = -5
4. Β = 5, Γ = 5, Δ = 1
- (2012-Β1, Β2012-Β1) Δίνεται το παρακάτω τμήμα αλγορίθμου:
Κ ← 1
Χ ← -1
i ← 0
Όσο Χ < 7 επανάλαβε
i ← i + 1
Κ ← Κ * Χ
Εμφάνισε Κ, Χ
Αν i mod 2 = 0 τότε
Χ ← Χ + 1
Αλλιώς
Χ ← Χ + 2
Τέλος_Αν
Τέλος_επανάληψηςΝα γράψετε στο τετράδιό σας τις τιμές που θα εμφανίσει το τμήμα αλγορίθμου κατά την εκτέλεσή του με τη σειρά που θα εμφανιστούν.
- (B2014-A5) Δίνεται το παρακάτω ημιτελές τμήμα αλγορίθμου:
A ← ...
B ← ...
Αρχή_επανάληψης
B ← ...
A ← ...
Μέχρις_ότου A > 200
Εμφάνισε B
Να ξαναγράψετε στο τετράδιό σας το παραπάνω τμήμα αλγορίθμου με τα κενά συμπληρωμένα, ώστε να υπολογίζει και να εμφανίζει το άθροισμα των περιττών ακεραίων από το 100 έως το 200.
- (ΕΒ2005-Θ2) Να αναπτύξετε έναν αλγόριθμο, ώστε
α) να διαβάζει έναν πραγματικό αριθμό μεγαλύτερο του μηδενός και μικρότερο του 1000 και να κάνει έλεγχο ορθής καταχώρησης του αριθμού,
β) να ελέγχει αν είναι ακέραιος και να εμφανίζει τη λέξη «ΑΚΕΡΑΙΟΣ» αλλιώς να εμφανίζει τη λέξη «ΠΡΑΓΜΑΤΙΚΟΣ»,
γ) να ελέγχει, στην περίπτωση που ο αριθμός είναι ακέραιος, αν είναι άρτιος ή περιττός και να εμφανίζει τη λέξη «ΑΡΤΙΟΣ» ή «ΠΕΡΙΤΤΟΣ» αντίστοιχα.
- (2020-B2) Ένας θετικός ακέραιος αριθμός μεγαλύτερος από το ένα (1) είναι πρώτος αν διαιρείται ακριβώς, μόνο με τον εαυτό του και τη μονάδα. Το παρακάτω τμήμα προγράμματος διαβάζει έναν θετικό ακέραιο αριθμό, ελέγχει αν είναι πρώτος ή όχι και εμφανίζει αντίστοιχο μήνυμα. Για το σκοπό αυτό διαβάζει έναν θετικό ακέραιο n (n>1), τον διαιρεί διαδοχικά με τους αριθμούς 2, 3, 4, …, n-1, ελέγχοντας μετά από κάθε διαίρεση αν ο αριθμός n διαιρείται ακριβώς.
Στην περίπτωση που διαιρείται ακριβώς, σταματάει η επαναληπτική διαδικασία και εμφανίζεται το μήνυμα ‘Δεν είναι πρώτος αριθμός’. Αν η επαναληπτική διαδικασία των διαιρέσεων τερματιστεί χωρίς ο αριθμός n να έχει διαιρεθεί ακριβώς από κανέναν αριθμό εμφανίζεται το μήνυμα ‘Είναι πρώτος αριθμός’. Ο αλγόριθμος περιέχει πέντε (5) αριθμημένα κενά. Να γράψετε στο τετράδιό σας τους αριθμούς των κενών και δίπλα ό,τι χρειάζεται να συμπληρωθεί, ώστε το τμήμα προγράμματος να λειτουργεί σωστά.
ΔΙΑΒΑΣΕ n
ΠΡΩΤΟΣ …(1)…
i<- …(2)…
ΑΡΧΗ_ΕΠΑΝΑΛΗΨΗΣ
ΑΝ …(3)… =0 ΤΟΤΕ
ΠΡΩΤΟΣ …(4)…
ΤΕΛΟΣ_ΑΝ
ii+1
ΜΕΧΡΙΣ_ΟΤΟΥ i>n-1 Ή …(5)…
AN ΠΡΩΤΟΣ = ΑΛΗΘΗΣ ΤΟΤΕ
ΓΡΑΨΕ ‘Είναι πρώτος αριθμός’
ΑΛΛΙΩΣ
ΓΡΑΨΕ ‘Δεν είναι πρώτος αριθμός’
ΤΕΛΟΣ_ΑΝ
- x