- (2009-Θ2) Δίνεται ο παρακάτω αλγόριθμος, στον οποίο έχουν αριθμηθεί οι εντολές εκχώρησης:
Αλγόριθμος Πολλαπλασιασμός
Δεδομένα //α,β//
Αν α>β τότε αντιμετάθεσε α, β
1 γ ← 0
Όσο α>0 επανάλαβε
2 δ ← α mod 10
Όσο δ>0 επανάλαβε
3 δ ← δ-1
4 γ ← γ+β
Τέλος_επανάληψης
5 α ← α div 10
6 β ← β*10
Τέλος_επανάληψης
Αποτελέσματα //γ//
Τέλος Πολλαπλασιασμός
Επίσης δίνεται υπόδειγμα πίνακα (πίνακας τιμών), με συμπληρωμένες τις αρχικές τιμές των μεταβλητών α,β (τιμές εισόδου), καθώς και της εντολής εκχώρησης με αριθμό 1.
| Αριθμός εντολής |
α |
β |
γ |
δ |
|
20 |
50 |
|
|
| 1 |
1 |
0 |
|
|
| …. |
|
|
|
|
Α. Να μετατρέψετε στο τετράδιό σας τον πίνακα και να τον συμπληρώσετε, εκτελώντας τον αλγόριθμο με αρχικές τιμές α=20, β=50 (που ήδη φαίνονται στον πίνακα).
Για κάθε εντολή εκχώρησης που εκτελείται να γράψετε σε νέα γραμμή του πίνακα:
α. Τον αριθμό της εντολής που εκτελείται (στην πρώτη στήλη).
β. Τη νέα τιμή της μεταβλητής που επηρεάζεται από την εντολή (στην αντίστοιχη στήλη).
Β. Να γράψετε τμήμα αλγορίθμου, που θα έχει το ίδιο αποτέλεσμα με την εντολή:
Αν α>β τότε αντιμεταθέστε α, β
Χωρίς να χρησιμοποιήσετε την εντολή αντιμετάθεσε.
- (EB2008-Θ1Γ) Δίνεται ο παρακάτω αλγόριθμος:
ΓΙΑ i ΑΠΟ ... ΜΕΧΡΙ n
ΓΙΑ j ΑΠΟ ... ΜΕΧΡΙ ... ΜΕ ΒΗΜΑ ...
ΑΝ A[j] ... A[j-1] ΤΟΤΕ
temp←A[j]
A[...]←A[...]
A[...]←temp
ΤΕΛΟΣ_ΑΝ
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
Να γράψετε στο τετράδιό σας τον παραπάνω αλγόριθμο κατάλληλα συμπληρωμένο, έτσι ώστε να υλοποιεί την ταξινόμηση της φυσαλίδας με αύξουσα σειρά.
- (2010-Α5) Δίνεται πίνακας Π[20] με αριθμητικές τιμές. Στις μονές θέσεις βρίσκονται καταχωρισμένοι θετικοί αριθμοί και στις ζυγές αρνητικοί αριθμοί. Επίσης, δίνεται το παρακάτω τμήμα αλγορίθμου ταξινόμησης τιμών του πίνακα.
Για x από 3 μέχρι 19 με_βήμα …..
Για y από …….. μέχρι ………. με_βήμα ……..
Αν Π[……..] < Π[ ……. ] Τότε
Αντιμετάθεσε Π[ y……] , Π[ …….]
Τέλος_αν
Τέλος_επανάληψης
Τέλος_επανάληψης
Να μεταφέρετε στο τετράδιό σας το παραπάνω τμήμα αλγορίθμου συμπληρώνοντας τα κενά με τις κατάλληλες σταθερές, μεταβλητές ή εκφράσεις, ώστε να ταξινομούνται σε αύξουσα σειρά μόνο οι θετικές τιμές του πίνακα.
- (B2016-A2) Να συμπληρώσετε τα κενά στον παρακάτω αλγόριθμο φυσαλίδα (ταξινόμηση ευθείας ανταλλαγής) σε έναν πίνακα table μεγέθους n.
Αλγόριθμος Φυσαλίδα
Δεδομένα // table, n //
Για i από ...(1)... μέχρι ...(2)...
Για j από ...(3)... μέχρι ...(4)... με βήμα ...(5)...
Αν table [j-1] > table [...(6)...] τότε
αντιμετάθεσε table [j-1], table [j]
Τέλος_αν
Τέλος_Επανάληψης
Τέλος_Επανάληψης
Αποτελέσματα // table //
Τέλος Φυσαλίδα
- (2014-B1) Για την ταξινόμηση, σε φθίνουσα σειρά, των στοιχείων ενός μονοδιάστατου πίνακα αριθμών Π[30] μπορεί να ακολουθηθεί η παρακάτω διαδικασία:Αρχικά, ο πίνακας σαρώνεται από την αρχή μέχρι το τέλος του, προκειμένου να βρεθεί το μεγαλύτερο στοιχείο του. Αυτό το στοιχείο τοποθετείται στην αρχή του πίνακα, ανταλλάσσοντας θέσεις με το στοιχείο της πρώτης θέσης του πίνακα. Η σάρωση του πίνακα επαναλαμβάνεται, ξεκινώντας τώρα από το δεύτερο στοιχείο του πίνακα. Το μεγαλύτερο από τα στοιχεία που απέμειναν ανταλλάσσει θέσεις με το στοιχείο της δεύτερης θέσης του πίνακα. Η σάρωση επαναλαμβάνεται, ξεκινώντας από το τρίτο στοιχείο του πίνακα, μετά από το τέταρτο στοιχείο του πίνακα κ.ο.κ. Το παρακάτω ημιτελές τμήμα αλγορίθμου κωδικοποιεί την παραπάνω διαδικασία:
Για k από 1 μέχρι 29
θ <- ...(1)... Για i από k μέχρι 30 Αν Π[i] >= Π[θ] τότε
θ <- ...(2)...
Τέλος_αν
Τέλος_επανάληψης
αντιμετάθεσε (4)..., (5)...
Τέλος_επανάληψης
Να γράψετε στο τετράδιό σας τους αριθμούς (1) έως (5), που αντιστοιχούν στα κενά του αλγορίθμου και, δίπλα σε κάθε αριθμό, ό,τι πρέπει να συμπληρωθεί, ώστε να γίνεται σωστά η ταξινόμηση.
- (2018-B1, B2018-B1) Το παρακάτω τμήμα αλγορίθμου αποτελεί μια παραλλαγή της ταξινόμησης φυσαλίδας, η οποία όμως σταματάει τις επαναλήψεις μόλις διαπιστώσει ότι ο πίνακας έχει ταξινομηθεί ως εξής: Μετά την ολοκλήρωση του εσωτερικού βρόχου, ελέγχει εάν έγιναν αντιμεταθέσεις στοιχείων και αν δεν έγιναν τότε ο αλγόριθμος τερματίζεται. Το τμήμα αλγορίθμου που δίνεται περιέχει κενά που έχουν αριθμηθεί.
i ← ... (1) ...
Αρχή_επανάληψης
stop ← ΑΛΗΘΗΣ
Για j από N μέχρι i με_βήμα -1
Αν table [j-1] > table [j] τότε
Αντιμετάθεσε table[j-1],table[j]
stop ← ... (2) ...
Τέλος_αν
Τέλος_επανάληψης
... (3) ...
Μέχρις_ότου i ... (4) ... N ή stop= ... (5) ...
Να γράψετε στο τετράδιό σας τους αριθμούς των κενών και δίπλα από κάθε αριθμό ό,τι πρέπει να συμπληρωθεί ώστε να επιτελείται η λειτουργία που περιγράφεται.
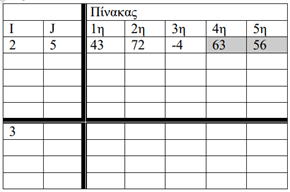
- (Β2002-Θ2) Ο μονοδιάστατος αριθμητικός πίνακας Table έχει τα ακόλουθα στοιχεία:
| 1η θέση |
2η θέση |
3η θέση |
4η θέση |
5η θέση |
| 43 |
72 |
-4 |
63 |
56 |
Δίνεται το παρακάτω τμήμα αλγορίθμου:
Για Ι από 2 μέχρι 5
Για J από 5 μέχρι Ι με βήμα -1
Αν Table[J-1] < Table[J] τότε
Αντιμετάθεσε Table[J-1], Table[J]
Τέλος_αν
Τέλος_επανάληψης
Τέλος_επανάληψης
Να μεταφερθεί στο τετράδιό σας ο ακόλουθος πίνακας και να συμπληρωθεί για όλες τις τιμές του J, που αντιστοιχούν σε I=2 και Ι=3.
- (E2001-04) Κατά τη διάρκεια Διεθνών Αγώνων Στίβου στον ακοντισμό έλαβαν μέρος δέκα (10) αθλητές. Κάθε αθλητής έκανε έξι (6) έγκυρες ρίψεις που καταχωρούνται ως επιδόσεις σε μέτρα. Να αναπτύξετε αλγόριθμο, ο οποίος:Α. εισάγει σε πίνακα δύο διαστάσεων τις επιδόσεις όλων των αθλητώνΒ. υπολογίζει και καταχωρεί σε μονοδιάστατο πίνακα την καλύτερη από τις επιδόσεις κάθε αθλητή.Γ. Ταξινομεί τις καλύτερες επιδόσεις των αθλητών που καταχωρήθηκαν στον μονοδιάστατο πίνακαΔ. βρίσκει την καλύτερη επίδοση του αθλητή που πήρε το χάλκινο μετάλλιο (τρίτη θέση).Παρατήρηση: Υποθέτουμε ότι όλες οι επιδόσεις είναι μεταξύ τους διαφορετικές.
